क्षेत्रमिति सूत्र त्रिविमीय आकृति|mensuration formula for 3D images
क्षेत्रमित के इस अध्याय के अंतर्गत किसी भी आकृति चाहे वह द्विविमिय हो या त्रिविमीय हैं उसका क्षेत्रफल( area) ,परिमाप(perimeter) तथा आयतन(volume) निकाल सकते है।
द्विविमिय आकृति ( 2D images) - द्विविमिय आकृति के अन्तर्गत वह सभी आकृतियां आती है जिसकी लंबाई ओर चौड़ाई होती है लेकिन उसकी ऊंचाई नहीं होती है। द्विविमिय आकृति के अंतर्गत वर्ग ,आयात , वृत तथा त्रिभुज जैसी आकृतियां आती है ।द्विविमिय आकृति के अन्तर्गत हम किसी भी आकृति का लंबाई, चौड़ाई, क्षेत्रफल तथा परिमाप ज्ञात करते हैं।
त्रिविमीय आकृति ( 3 D images) - त्रिविमीय आकृति के अंतर्गत वह सभी आकृतियां आती है इसकी लंबाई चौड़ाई के साथ-साथ ऊंचाई भी होती है। जैसे- घन, घनाभ, गोला, शंकु, बेलन इत्यादि। त्रिविमीय आकृति के अंतर्गत हम किसी भी आकृति की लंबाई, चौड़ाई, ऊंचाई, क्षेत्रफल, परिमाप, तथा आयतन ज्ञात करते हैं।
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
साथ ही त्रिविमीय आकृति में किसी भी आकृति का वक्र पृष्ठीय क्षेत्रफल तथा सम्पूर्ण पृष्ठीय क्षेत्रफल निकाला जाता है।
वक्र पृष्ठीय क्षेत्रफल ( Curve surface area) - वक्र पृष्ठीय क्षेत्रफल वह होता है जिसमें उसके आधार को छोड़कर बाकी सभी फलको का क्षेत्रफल निकाला जाता है, जैसे बेलन में उसके चेहरे तथा आधार दोनों अलग अलग होता है बेलन का आधार वृत्ताकार तथा उसके फलके बेलनाकार होती है। इसमें बेलन के संपूर्ण बेलनाकार फल्को को वक्र पृष्ठीय क्षेत्रफल कहते हैं।
संपूर्ण पृष्ठीय क्षेत्रफल (Entire page area) - संपूर्ण पृष्ठीय क्षेत्रफल के अंतर्गत किसी भी आकृति की सभी पलकों के साथ-साथ उसके आधार के क्षेत्रफल को भी जोड़ा जाता है इसे ही संपूर्ण पृष्ठीय क्षेत्रफल कहते हैं। जैसे बेलन के संपूर्ण बेलनाकार फलको का क्षेत्रफल जिसे बेलन का वक्र पृष्ठीय क्षेत्रफल कहते हैं तथा उसके वृत्ताकार आधार का क्षेत्रफल ,दोनों मिलकर बेलन का संपूर्ण पृष्ठीय क्षेत्रफल बनाते हैं।
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
आज के इस अध्याय में हम त्रिविमीय आकृति के सभी सूत्रों को जानेंगे और कुछ प्रश्नों को हल करेंगे।
1) घन (cube) :- यह वर्ग का 3D चित्र होता है जिसमें लंबाई, चौड़ाई के साथ साथ ऊंचाई भी होती है। इसकी सभी भुजाएं बराबर होती है अर्थात इसकी लंबाई, चौड़ाई और ऊंचाई तीनों बराबर होती है उसे घन कहते है।
- फलक (faces) :- 6
- शीर्ष ( vertix) :- 8
- भुजाएं (sides) :- 12
घन में क्षेत्रफल, परिमाप तथा आयतन निकाला जाता है, साथ ही इसमें घन का वक्र पृष्ठीय क्षेत्रफल तथा संपूर्ण पृष्ठीय क्षेत्रफल निकाला जाता है। तथा इसकी लंबाई ,चौड़ाई, तथा ऊंचाई तीनों बराबर होती है।
- घन का संपूर्ण पृष्ठीय क्षेत्रफल (Entire page area of cube) = 6a²
जहा (a) = भुजाएं ( sides)
- घन का वक्र पृष्ठीय क्षेत्रफल या चार दीवारों का क्षेत्रफल (Curve surface area of cube or area of four walls) = 4a²
जहा (a) = भुजाएं ( sides)
- घन का आयतन (volume of cube) = a³
जहा (a) = भुजाएं ( sides)
- घन का विकर्ण ( diagonal of cube ) = √ 3 a
जहा (a) = भुजाएं ( sides)
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
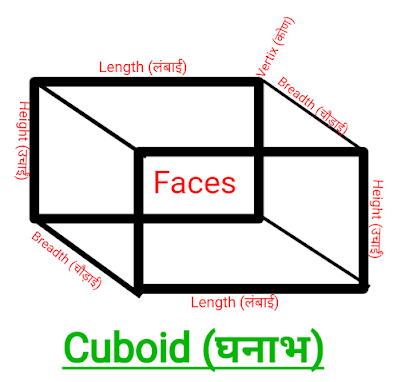
2) घनाभ ( cuboid) - यह आयत का 3D चित्र होता है जिसमें लंबाई, चौड़ाई के साथ साथ ऊंचाई भी होती है। इसकी दो-दो भुजाएं बराबर होती है। अर्थात इसकी लंबाई, चौड़ाई और ऊंचाई तीनों का माप अलग अलग होता है, उसे घनाभ कहते है।
- फलक (faces) :- 6
- शीर्ष ( vertix) :- 8
- भुजाएं (sides) :- 12
घनाभ में क्षेत्रफल, परिमाप तथा आयतन निकाला जाता है साथ ही इसमें घनाभ का वक्र पृष्ठीय क्षेत्रफल तथा संपूर्ण पृष्ठीय क्षेत्रफल निकाला जाता है। तथा इसकी लंबाई ,चौड़ाई, तथा ऊंचाई तीनों का माप अलग अलग होता है।
- घनाभ का संपूर्ण पृष्ठीय क्षेत्रफल (Entire page area of cuboid) = 2( lb + bh + hl )
जहा ( l ) = लंबाई (length)
जहा ( b ) = चौड़ाई (breadth)
जहा ( h ) = ऊंचाई (height)
- घनाभ का वक्र पृष्ठीय क्षेत्रफल या चार दीवारों का क्षेत्रफल (Curve surface area of cuboid or area of four walls) = 2h ( l+b )
जहा ( l ) = लंबाई (length)
जहा ( b ) = चौड़ाई (breadth)
जहा ( h ) = ऊंचाई (height)
- घनाभ का आयतन (volume of cuboid) = l×b×h
जहा ( l ) = लंबाई (length)
जहा ( b ) = चौड़ाई (breadth)
जहा ( h ) = ऊंचाई (height)
- घनाभ का विकर्ण ( diagonal of cuboid ) = √ l² + b² + h²
जहा ( l ) = लंबाई (length)
जहा ( b ) = चौड़ाई (breadth)
जहा ( h ) = ऊंचाई (height)
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
3) बेलन (cylinder) - इस आकृति में सिर्फ एक ही बेलनाकार फलक होता है जिससे पूरी आकृति बनी होती है। तथा इसके दो आधार होते है तथा इसका आधार वृत्ताकार होता है। इसमें बेलन का वक्र पृष्ठीय क्षेत्रफल तथा संपूर्ण पृष्ठीय क्षेत्रफल निकाला जाता है। बेलन में कोई भी शीर्ष नहीं होता है, लेकिन बेलन का एक वक्राकार फलक होता है।
बेलन में ऊंचाई तथा इसके आधार की त्रिज्या ज्ञात किया जाता है। जिससे ही बेलन का क्षेत्रफल, आयतन तथा परिमाप निकाला जाता है।
- बेलन का संपूर्ण पृष्ठीय क्षेत्रफल (Entire page area of cylinder) = 2 πr ( h + r )
जहा (r) = आधार की त्रिज्या (radius)
जहा (h) = बेलन की ऊंचाई ( height)
- बेलन का वक्र पृष्ठीय क्षेत्रफल (Curve surface area of cylinder) = 2πrh
जहा (r) = आधार की त्रिज्या (radius)
जहा (h) = बेलन की ऊंचाई ( height)
- बेलन का आयतन (volume of cylinder)। = πr²h
जहा (r) = आधार की त्रिज्या (radius)
जहा (h) = बेलन की ऊंचाई ( height)
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
खोखला बेलन ( hollow cylinder)= बेलन में खोखले बेलन का भी आयतन निकाला जाता है , खोखला बेलन वह होता है जिसमें बेलन को बीच से काट कर निकाल देने के पश्चात जो बच जाता है उसे ही खोखला बेलन कहते हैं।
- खोखला बेलन का आयतन ( volume of hollow cylinder) = π (R² - r²) h
जहा (R) = बड़े वृत का त्रिज्या
जहा ( r) = छोटे या आंतरिक वृत की त्रिज्या
जहा (h) = बेलन की ऊंचाई
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
4) शंकु ( cone) - यह त्रिभुज का 3D चित्र होता है जिसमें लंबवत ऊंचाई के साथ तिर्यक ऊंचाई भी होती है। तथा शंकु एक आधार होता है और वह वृत्ताकार होता है। और इसका एक शीर्ष होता है। तथा शंकु का एक वक्राकार फलक होता है।
- फलक (faces) :- 1
- शीर्ष ( vertix) :- 1
- भुजाएं (sides) :- 0
शंकु में लंबवत ऊंचाई, तिर्यक ऊंचाई, संपूर्ण पृष्ठीय क्षेत्रफल, वक्र पृष्ठीय क्षेत्रफल तथा आयतन निकाला जाता है।
- तिर्यक ऊंचाई (Oblique height) ( L) = √ r² + h²
जहा (l) = तिर्यक ऊंचाई
जहा (r) = आधार की त्रिज्य
जहा (h) = लंबवत ऊंचाई ( Vertical height)
- शंकु का संपूर्ण पृष्ठीय क्षेत्रफल (Entire page area of cone) = πrl + πr²
जहा (l) = तिर्यक ऊंचाई
जहा (r) = आधार की त्रिज्या
- शंकु का वक्र पृष्ठीय क्षेत्रफल (Curve surface area of cone) = πrl
जहा (l) = तिर्यक ऊंचाई
जहा (r) = आधार की त्रिज्या
- शंकु का आयतन (volume of cone) = 1/3 πr²h
जहा (l) = तिर्यक ऊंचाई
जहा (r) = आधार की त्रिज्या
जहा ( h) = लंबवत ऊंचाई
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
5) गोला ( sphere) = यह वृत्त की 3D आकृति होती है। वृत्त की ही तरह इसमें भी कोई कोना नहीं होता है, और ना ही इसकी लंबाई व चौड़ाई होती है। इसमें वृत्त की ही तरह त्रिज्या और व्यास निकाला जाता है। लेकिन इसका सिर्फ एक वक्राकार फलक होता है।
गोले में सिर्फ क्षेत्रफल तथा आयतन निकाला जाता है। गोले का संपूर्ण पृष्ठीय क्षेत्रफल और वक्र पृष्ठीय क्षेत्रफल दोनों एक ही होता है क्योंकि गोले में कोई आधार नहीं होता है।
- गोले का पृष्ठीय क्षेत्रफल ( area of sphere) = 4πr²
जहा (r) = गोले की त्रिज्या (radius)
- गोले का आयतन ( volume of sphere) = 4/3 πr³
जहा (r) = गोले की त्रिज्या (radius)
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
6) अर्ध गोला (semi sphere)= गोले को आधा कर देने पर अर्ध गोला प्राप्त होता है। अर्ध गोला में एक आधार होता है तथा इसमें व्यास और त्रिज्या निकाला जाता है और इसलिए अर्ध गोला में वक्र पृष्ठ क्षेत्रफल तथा संपूर्ण पृष्ठीय क्षेत्रफल दोनों ही निकाला जाता है।
अर्ध गोला में वक्र पृष्ठीय क्षेत्रफल, संपूर्ण पृष्ठीय क्षेत्रफल के साथ-साथ आयतन भी निकाला जाता।
- अर्ध गोला का वक्र पृष्ठीय क्षेत्रफल (Curve surface area of semi sphere) = 2πr²
जहा (r) = त्रिज्या ( radius)
- अर्ध गोला का संपूर्ण पृष्ठीय क्षेत्रफल (Entire page area of semi sphere) = 3πr²
जहा (r) = त्रिज्या ( radius)
- अर्ध गोले का आयतन ( volume of semi sphere) = 2/3 πr³
जहा (r) = त्रिज्या ( radius)
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
7) खोखला गोला (hollow sphere) = जब गोले के बीच वाले भाग को काटकर निकाल दिया जाता है, तथा बचा हुआ भाग खोखला गोला कहलाता है। खोखले गोले का भी गोले कि तरह ही संपूर्ण पृष्ठीय क्षेत्रफल तथा वक्र पृष्ठीय क्षेत्रफल एक ही होता है क्योंकि इसमें कोई आधार नहीं होता है। खोखला गोला गाड़ी के टायरो की तरह दिखाई देता है।
खोखले गोले में क्षेत्रफल तथा आयतन निकाला जाता है।इसमें दो त्रिज्या होती है एक बड़े गोले की त्रिज्या तथा दूसरा गोले की काटकर अंदर बने गोले की त्रिज्या।
- खोखला गोला का संपूर्ण पृष्ठीय क्षेत्रफल (Entire page area of hollow sphere) = 4π ( R² - r² )
जहा (R) = बड़े गोले की त्रिज्या
जहा (r) = छोटे गोले कि त्रिज्या
- खोखले गोले का आयतन ( volume of hollow sphere) = 4/3π (R ³ - r ³)
जहा (R) = बड़े गोले की त्रिज्या
जहा (r) = छोटे गोले कि त्रिज्या
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
8) प्रिजम (prism) = प्रिज्म कई तरह के होते है। प्रिज्म का आधार एवं छत समबाहु त्रिभुज होता है या फिर कभी कभी प्रिज्म का आधार एवं छत वर्गाकार भी हो सकता है।
- प्रिज्म के आधार एवं छत समबाहु त्रिभुज होती है।
- प्रिज्म के बाकी की फल्के आयताकार होते हैं।
- कभी कभी प्रिज्म का आधार वर्गाकार भी ही सकता है।
प्रिज्म में वक्र पृष्ठीय क्षेत्रफल तथा संपूर्ण पृष्ठीय क्षेत्रफल एवं आयतन निकाला जाता है। प्रिज्म में लंबाई चौड़ाई तथा ऊंचाई तीनों ही होते हैं। तथा तीनों का माप अलग-अलग होता है। प्रिज्म का आधार समबाहु त्रिभुज होता है जिसके कारण इसके आधार की भुजाएं बराबर होती है लेकिन इसकी फलके जो कि आयताकार होती है इसलिए उसकी लंबाई चौड़ाई तथा ऊंचाई अलग-अलग होती है।
- प्रिज्म का वक्र पृष्ठीय क्षेत्रफल (Curve surface area of prism) = आधार का परिमाप × ऊंचाई
आधार का परिमाप अर्थात समबाहु त्रिभुज का
परिमाप, समबाहु त्रिभुज का परिमाप = 3a
जहा (a) = समबाहु त्रिभुज की भुजाएं)
ऊंचाई = प्रिज्म की ऊंचाई।
- या 3 × लंबाई× चौड़ाई , जहा (लंबाई × चौड़ाई = आयत का क्षेत्रफल)
- प्रिज्म का संपूर्ण पृष्ठीय क्षेत्रफल (Entire page area of prism) = आधार का परिमाप × ऊंचाई + आधार का क्षेत्रफल
= 3a×h + 2(A)
जहा 3a = आधार का परिमाप अर्थात समबाहु
त्रिभुज का परिमाप
जहा A = आधार का क्षेत्रफल अर्थात समबाहु
त्रिभुज का क्षेत्रफल = √3 a² /4
जहा h = ऊंचाई
- या आयात का क्षेत्रफल + आधार का क्षेत्रफल 3 ( l×b ) + 2 (A)
3(l×b) = तीन आयत का क्षेत्रफल
2 ( A ) = दो आधार का क्षेत्रफल
- प्रिज्म का आयतन ( volume of prism) = A × h
जहा ( A ) = आधार का क्षेत्रफल = √3 a² /4
जहा ( h ) = ऊंचाई
क्षेत्रमिति सूत्र त्रिविमीय आकृति| mensuration formula for 3D images
9) पिरामिड ( pyramid) = पिरामिड शंकु की तरह दिखने वाला लेकिन उससे अलग होता है इसकी फलके शंकु की तरह चिकनी और केवल एक फलक नहीं होती है ,बल्कि इसकी फलक कई त्रिभुजों से मिलकर बनी होती है, इसलिए इसकी कई फलके होती है तथा इसका शंकु की तरह वृत्ताकार नहीं बल्कि बहुभूज होता है।
पिरामिड का आधार बहुभुज जैसे पंचभूज, षट्भुज , अष्टभुज कुछ भी हो सकता है और जितनी भी भुजाओं वाली आधार होगी उतनी ही इसकी फ़लके भी होगी।
पिरामिड में वक्र पृष्ठीय क्षेत्रफल तथा संपूर्ण पृष्ठीय क्षेत्रफल एवं आयतन निकाला जाता है। और इसमें एक शीर्ष ,कई फलके तथा एक बहुभुज आधार होता है। प्रिज्म में त्रिज्या, तिर्यक ऊंचाई तथा लंबवत ऊंचाई निकाल जाती है।
- तिर्यक ऊंचाई ( l ) = √ h² + r²
- लंबवत ऊंचाई ( h ) = √ l² - r²
जहा ( l ) = तिर्यक ऊंचाई
जहा ( h ) = लंबवत ऊंचाई
जहा ( r ) = आंतरिक त्रिज्या
- पिरामिड का वक्र पृष्ठीय क्षेत्रफल (Curve surface area of Pyramid) = 1/2 × आधार का परिमाप × तिर्यक ऊंचाई
- पिरामिड का संपूर्ण पृष्ठीय क्षेत्रफल (Entire page area of Pyramid) = वक्र पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल
- पिरामिड का आयतन ( volume of Pyramid) = 1/3 × आधार का क्षेत्रफल × ऊंचाई
नोट : आधार का परिमाप और क्षेत्रफल में षट्भुज का क्षेत्रफल लगेगा या जो भी बहूभूज का आधार होगा उसी का क्षेत्रफल और परिमाप लगेगा।
यदि आपके मन में कोई प्रश्न, कोई शिकायत या सुझाव हो तो आप हमें comment कर सकते हैं। आपके प्रश्न,सुझावऔर शिकायत हमारे लिए महत्वपूर्ण है ,हम आपके सवालों के जवाब देने को तत्पर है। और अगर आपको ये पसंद आया तो ऊपर सदस्यता पर क्लिक करके betrendiiii की सदस्यता जरूर ले, और हमें प्रोत्साहित करे।
Betrendiiii रखे आपको हमेशा trend में।
धन्यवाद









टिप्पणियाँ
एक टिप्पणी भेजें